[PR]
×
[PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
平成26年度・神奈川県の公立高校入試を解いてみた(数学だけ)
さて今年も、朝刊に、平成26年度の神奈川県の公立高校入試問題が入っていたので、
解いてみました。
今年は雪が降っていたため、朝刊が届くの遅い&寝てないという悪条件が重なり、
自己最低記録となりました。(言い訳)
去年と同じく、記述問題が2問あります。
個人的な感想ですが、これは…全体的には、皆さん、時間が足りないのではないか?と
思いました。
去年より、多少詳しく解説します。
問1:計算するだけ。簡単だと思います。
問2:(エ)は、「対称式」と呼ばれているもので、x + y = 2√6、x*y = 2 を先に計算して
おきます。
(ク)は…。これは、解き方がすぐに思いつかなかったら、後回しにすべき問題だと
思います。 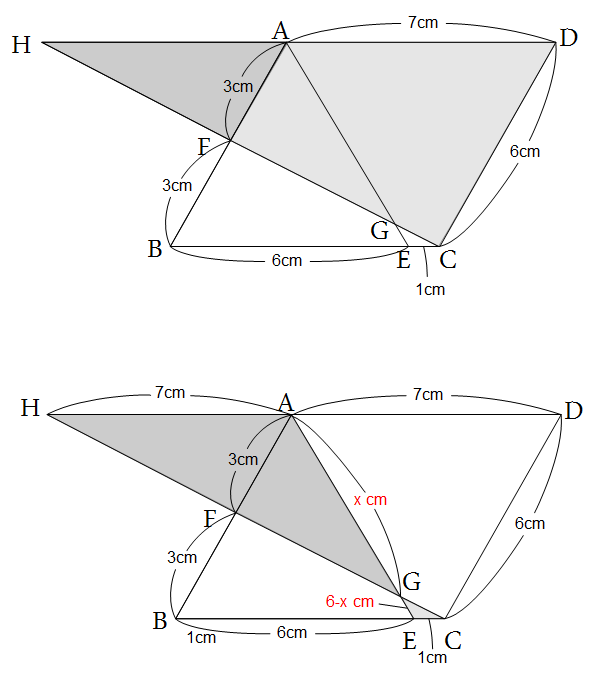 DAを延長し、CFも延長して、できた交点をHとすると、△HAFと△HDAは相似で、
DAを延長し、CFも延長して、できた交点をHとすると、△HAFと△HDAは相似で、
相似比は1:2です。よってHAは7cm。
次に、△HAGと△CEGも相似で、相似比は7:1なので、AG:(6 - AG) = 7:1 となり、
これを解くと、21/4 となります。
問3:(ア)は、点Dの座標を求めれば出せます。まず、y = x^2 の各座標を求めます。
AE:ED = 4:3 より、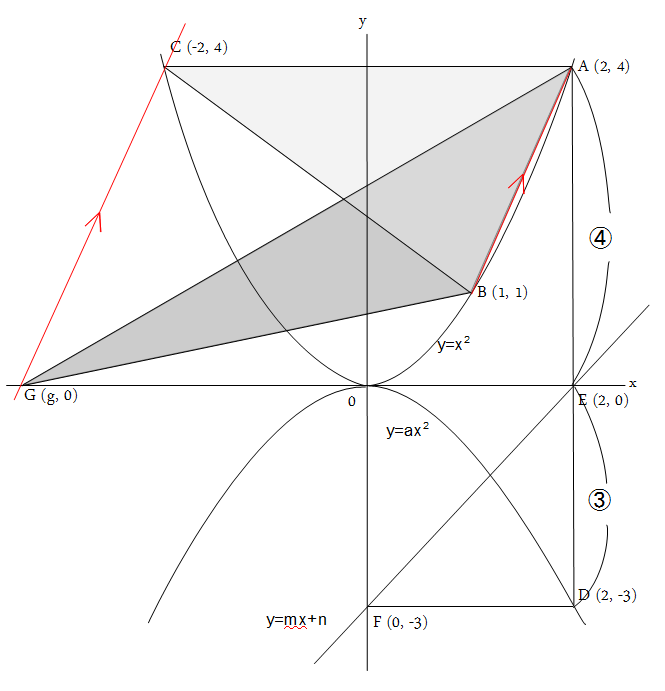 D(2, -3) となるので、これを y = a*x^2 に代入して a を求めると、a = -3/4 と
D(2, -3) となるので、これを y = a*x^2 に代入して a を求めると、a = -3/4 と
出ます。
(イ)は、F(0, -3)、E(2, 0) の2点を通る直線なので、傾きは 3/2、切片は -3 より、
y = 3/2*x - 3 と出せます。
(ウ)は、ここでは「等積変形」を用いるのが定石でしょう。△ABCと△ABGは、
辺ABを共有しているので、辺ABに平行で、点Cを通る直線上に点Gがあれば、
互いの面積は等しくなります。
直線ABの傾きは、計算すると 3 になるので、これと同じ傾きの直線が、
点C(-2, 4)を通ればいいわけです。
y = 3x + b の x, y にこの座標を代入して b を求めると、y = 3x + 10 となります。
後は、y = 0 のときの x が求める点Gのx座標となり、それは -10/3 となります。
よって、G(-10/3, 0)。
問4:この手のさいころを2つ振る問題は、6x6のマトリクスを描いて、そこに値を
書き込むのが定石ですが、この問題に限って言うと、それでは時間がかかって
しまうので、止めるべきでしょう。
(ア)は、2つのさいころの目を足すと、2~12 までの値になるので、該当する
「5の倍数」は、5 と 10 になります。それぞれ、(4, 1), (3, 2), (2, 3), (1, 4) と
(6, 4), (5, 5), (4, 6) があるので、合計7通り。よって答えは 7/36。
(イ)は、210 を素因数分解すると、2*3*5*7 と、何だか素数を並べたような作為的な
数字が出てきます。これを組み合わせて 11~66 までの数を作ると、
(2, 3, 5), (2, 3, 7), (2, 7), (3, 5), (3, 7), (5, 7) の組み合わせが考えられます。
しかし!
(2, 3, 5) は、30 となるので、1の位が0になってしまい、さいころ的に
ありえません。なので、これを除くと、答えは 5/36。
(ウ)は、111 = 3*37 と、これまた作為的な数字が出てきます。よって
ルートの中は、3*(37 - n) となります。これの (37 - n) が、
3*1^2 = 3 、3*2^2 = 12 、3*3^2 = 27 、3*4^2 = 48 … となればいいわけ
ですが、さいころの目からして、36より大きい数の 48 以降はありえないので、
合計3つということになり、答えは 3/36 = 1/12。
(n は計算しないように。時間の無駄です)
問5:これは、書くのに時間がかかります。それと、問題の文章から式を立てるのが苦手な
人には、解けない問題だと思います。しかし内容は、単なる連立方程式です。
Aさんが、家からC商店まで上昇するのに x/50 分、C商店からBさんの家まで
下降するのに y/60 分、勉強したのが 60 分、Bさんの家からC商店まで上昇したのが
y/50 分、C商店で 5 分、そして、再びC商店からBさんの家まで下降するのに
y/60 分かかっています。
8時から9時39分までは、1時間39分 = 99 分。
つまり、
x/50 + y/60 + 60 + y/50 + 5 + y/60 = 99 …(1)
変形すると、
x/50 + y/30 + y/50 = 34, 3*x + 5*y + 3*y = 34*150,
3*x + 8*y = 5100 …(2)
一方、距離で言うと、x + y = 1200 …(3)
なので、(2) と (3) を連立方程式で解くと、x = 900, y = 300 メートルと出ます。
問6:(ア)は、計算するだけです。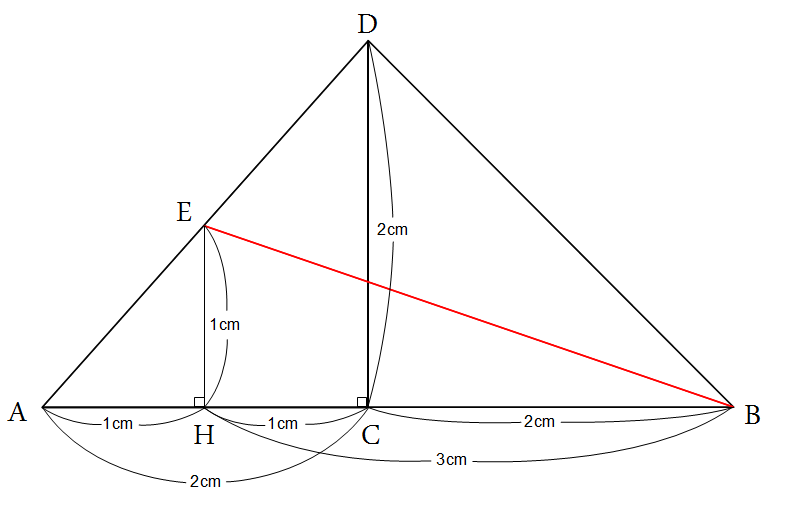 (イ)は、上の展開図のように考えると、EH^2 = 1、BH^2 = 9 となるので、
(イ)は、上の展開図のように考えると、EH^2 = 1、BH^2 = 9 となるので、
BE = √10。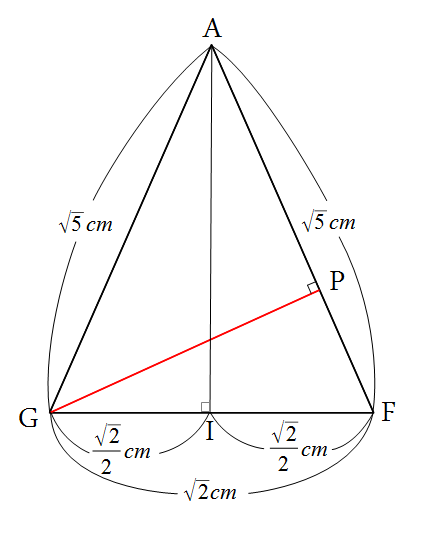 (ウ)は、△AGFが、上の図のような二等辺三角形になることを考えると、
(ウ)は、△AGFが、上の図のような二等辺三角形になることを考えると、
AI^2 = 5 - 1/2 = 9/2、
AI = 3/√2 となるので、△AGFの面積は、√2*3/√2/2 = 3/2 となります。
ここで、AFを底辺と見ると、√5xGP/2 = △AGF = 3/2 なので、
GP = 3/√5 = 3√5/5。
問7:公表された答えとは異なっていましたが、合っているはずです。
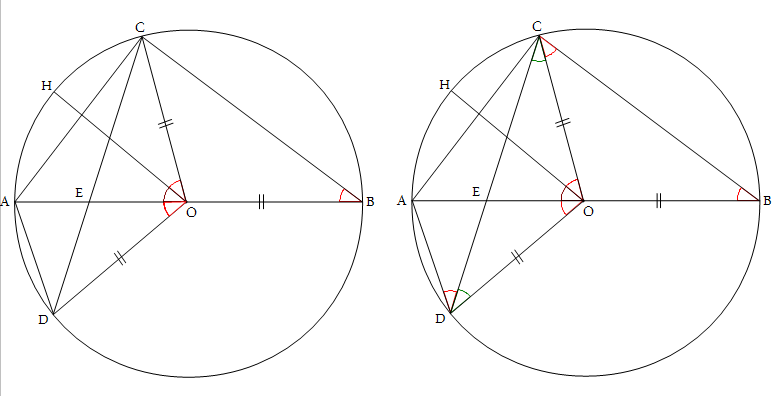
まず、∠COAの二等分線を引き、それと弧ACが交わる点を、H とします。
円周角の性質と仮定から、∠DOA = ∠HOA = ∠COH = ∠CBA …(1)
弧CAに対する円周角なので、∠CBA = ∠CDA …(2)
△OBCは二等辺三角形なので、∠CBA = ∠OCB …(3)
△OCDも二等辺三角形なので、∠OCD = ∠ODC …(4)
∠ODA = ∠ODC + ∠ODC …(5)
∠BCA = ∠OCB + ∠OCD …(6)
(3)、(4) から (5)、(6) は、∠ODA = ∠BCA …(7)
(1)、(2)、(7) より、対応する2つの角が等しいので、△OAD ∽ △BCE。
※弧DBに対する円周角から、∠OAD = ∠BCE とやったほうが速い。これが、
公表された答えです。
ちなみに僕は、解くのに50分では足りませんでした。結果は74点。
今まで解いた中で、最低の得点率でした。
問5の立式にケアレスミスがあり、それだけで10点全て落としてしまいました。
その他、確率の問題を読み間違えていたりと、散々でした。
睡眠はよく取りましょう。
解いてみました。
今年は雪が降っていたため、朝刊が届くの遅い&寝てないという悪条件が重なり、
自己最低記録となりました。(言い訳)
去年と同じく、記述問題が2問あります。
個人的な感想ですが、これは…全体的には、皆さん、時間が足りないのではないか?と
思いました。
去年より、多少詳しく解説します。
問1:計算するだけ。簡単だと思います。
問2:(エ)は、「対称式」と呼ばれているもので、x + y = 2√6、x*y = 2 を先に計算して
おきます。
そして、x^2*y + x*y^2 = xy(x + y) と因数分解して代入すれば、4√6 と出ます。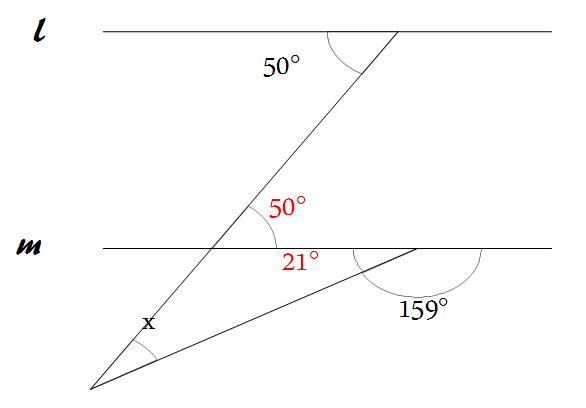
(キ)は、上の図のように角度を求めれば、x = 50°- 21°= 29°と出ます。(ク)は…。これは、解き方がすぐに思いつかなかったら、後回しにすべき問題だと
思います。
相似比は1:2です。よってHAは7cm。
次に、△HAGと△CEGも相似で、相似比は7:1なので、AG:(6 - AG) = 7:1 となり、
これを解くと、21/4 となります。
問3:(ア)は、点Dの座標を求めれば出せます。まず、y = x^2 の各座標を求めます。
AE:ED = 4:3 より、
出ます。
(イ)は、F(0, -3)、E(2, 0) の2点を通る直線なので、傾きは 3/2、切片は -3 より、
y = 3/2*x - 3 と出せます。
(ウ)は、ここでは「等積変形」を用いるのが定石でしょう。△ABCと△ABGは、
辺ABを共有しているので、辺ABに平行で、点Cを通る直線上に点Gがあれば、
互いの面積は等しくなります。
直線ABの傾きは、計算すると 3 になるので、これと同じ傾きの直線が、
点C(-2, 4)を通ればいいわけです。
y = 3x + b の x, y にこの座標を代入して b を求めると、y = 3x + 10 となります。
後は、y = 0 のときの x が求める点Gのx座標となり、それは -10/3 となります。
よって、G(-10/3, 0)。
問4:この手のさいころを2つ振る問題は、6x6のマトリクスを描いて、そこに値を
書き込むのが定石ですが、この問題に限って言うと、それでは時間がかかって
しまうので、止めるべきでしょう。
(ア)は、2つのさいころの目を足すと、2~12 までの値になるので、該当する
「5の倍数」は、5 と 10 になります。それぞれ、(4, 1), (3, 2), (2, 3), (1, 4) と
(6, 4), (5, 5), (4, 6) があるので、合計7通り。よって答えは 7/36。
(イ)は、210 を素因数分解すると、2*3*5*7 と、何だか素数を並べたような作為的な
数字が出てきます。これを組み合わせて 11~66 までの数を作ると、
(2, 3, 5), (2, 3, 7), (2, 7), (3, 5), (3, 7), (5, 7) の組み合わせが考えられます。
しかし!
(2, 3, 5) は、30 となるので、1の位が0になってしまい、さいころ的に
ありえません。なので、これを除くと、答えは 5/36。
(ウ)は、111 = 3*37 と、これまた作為的な数字が出てきます。よって
ルートの中は、3*(37 - n) となります。これの (37 - n) が、
3*1^2 = 3 、3*2^2 = 12 、3*3^2 = 27 、3*4^2 = 48 … となればいいわけ
ですが、さいころの目からして、36より大きい数の 48 以降はありえないので、
合計3つということになり、答えは 3/36 = 1/12。
(n は計算しないように。時間の無駄です)
問5:これは、書くのに時間がかかります。それと、問題の文章から式を立てるのが苦手な
人には、解けない問題だと思います。しかし内容は、単なる連立方程式です。
Aさんが、家からC商店まで上昇するのに x/50 分、C商店からBさんの家まで
下降するのに y/60 分、勉強したのが 60 分、Bさんの家からC商店まで上昇したのが
y/50 分、C商店で 5 分、そして、再びC商店からBさんの家まで下降するのに
y/60 分かかっています。
8時から9時39分までは、1時間39分 = 99 分。
つまり、
x/50 + y/60 + 60 + y/50 + 5 + y/60 = 99 …(1)
変形すると、
x/50 + y/30 + y/50 = 34, 3*x + 5*y + 3*y = 34*150,
3*x + 8*y = 5100 …(2)
一方、距離で言うと、x + y = 1200 …(3)
なので、(2) と (3) を連立方程式で解くと、x = 900, y = 300 メートルと出ます。
問6:(ア)は、計算するだけです。
BE = √10。
AI^2 = 5 - 1/2 = 9/2、
AI = 3/√2 となるので、△AGFの面積は、√2*3/√2/2 = 3/2 となります。
ここで、AFを底辺と見ると、√5xGP/2 = △AGF = 3/2 なので、
GP = 3/√5 = 3√5/5。
問7:公表された答えとは異なっていましたが、合っているはずです。
まず、∠COAの二等分線を引き、それと弧ACが交わる点を、H とします。
円周角の性質と仮定から、∠DOA = ∠HOA = ∠COH = ∠CBA …(1)
弧CAに対する円周角なので、∠CBA = ∠CDA …(2)
△OBCは二等辺三角形なので、∠CBA = ∠OCB …(3)
△OCDも二等辺三角形なので、∠OCD = ∠ODC …(4)
∠ODA = ∠ODC + ∠ODC …(5)
∠BCA = ∠OCB + ∠OCD …(6)
(3)、(4) から (5)、(6) は、∠ODA = ∠BCA …(7)
(1)、(2)、(7) より、対応する2つの角が等しいので、△OAD ∽ △BCE。
※弧DBに対する円周角から、∠OAD = ∠BCE とやったほうが速い。これが、
公表された答えです。
ちなみに僕は、解くのに50分では足りませんでした。結果は74点。
今まで解いた中で、最低の得点率でした。
問5の立式にケアレスミスがあり、それだけで10点全て落としてしまいました。
その他、確率の問題を読み間違えていたりと、散々でした。
睡眠はよく取りましょう。
PR
コメント
忍者カウンター
カレンダー
最新記事
(05/08)
(04/10)
(03/26)
(03/22)
(03/12)
プロフィール
HN:
PascalChan
性別:
男性
趣味:
引きこもり
ブログ内検索
P R
