[PR]
×
[PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
計算するまでもない問題・その3
さて、今回の計算の不要な問題は、またまた鈴木貫太郎さんのYouTubeの動画からです。
東工大 高校数学
さすが東工大。問題がくだらない。
東工大に行く奴なんて、未成年なのにタバコを吸っている不良か、髪の毛がリーゼントの
落ちこぼれか、ニート予備軍ばかりなので、こういう計算するまでもない問題を出さないと、
受験生が答案に何も書けなくなってしまうのでしょう。
2ちゃん(今は「5ちゃんねる」ですが)の有名な信州大コピペにもある通りです。
大体就職先も、
テロリストに爆破されたことがある危険な鉄工所とか、
(僕は個人的には2SC1815とか2SK241とか2SK1530とかは大好きですけど)
不正会計のせいで儲かる事業を売る羽目になった電機会社とか、
聞いたこともない工務店とか、
これまた聞いたこともない電線屋とか、
京都の花札屋みたいな会社とか、
世間一般の価値観で言うなら、ろくなところがありません。
それでも就職できるのはまだいいほうで、僕みたいに対人恐怖だと、くまみこ第11話で、
雨宿まちがセンダイでアイドルコンテストのリハーサルに出たときに、
と言ってしまったように、緊張して見当はずれなことを言ってしまうせいか、
面接で弾かれて、どこにも就職できず、ニートまっしぐらです。
そういう人は、仕方がないのでアルバイトをしようとするわけですが、
履歴書に「東工大卒」と書くと、大抵どこでも、嫌な顔をされたり、
「君にはもっといい働き口があるよ~」などと言われて、面接で落とされます。
だからニートのまま。
学歴がスティグマになる大学なんて、東工大くらいのものでしょう。
ビリー・ジョエルの曲に、「Allentown」というのがありますが、
Billy Joel - Allentown (Official Video)
その中で
ゼロです。
ところが、東工大の学歴はスティグマ、つまりマイナスになってしまう
のです。
それと比較すると、例えば、京都大学の工学部は素晴らしい。
アニメ系の作曲家一つ取っても、例えば、神前暁さんのような有名な人がいます。
東工大出身者に、こういう有名な人、いますか? いないでしょ?
それが全ての答えです。
まあそれはともかく、問題の説明をしましょう。
出題は1977年と古いものです。
この式は、
(1+(x/m)/m)^m = (1+(x/m)/m)^(m/(x/m)*(x/m))
= ((1+(x/m)/m)^(m/(x/m)))^(x/m)
と変形できますが、(1+(x/m)/m)^(m/(x/m)) は
自然対数の底eの定義式と似ているので、近似して
e^(x/m)
と変形できます。e^t と t の増加・減少は一致するので、
m が大きくなれば、元の式が小さくなることは自明です。
よって、(1+x/m^2)^m > (1+x/n^2)^n とわかります。
でも、(受験)数学的には、それでは説明不足ということなのかも知れません。
YouTubeの動画の鈴木貫太郎さんのように、いちいち数式をいじって「証明」する
必要があるのでしょう。
もちろん、鈴木貫太郎さんの解き方とは別に、f(y)=(1+x/y^2)^y とおいて、
yについて微分して増減表を書き、f(y) の大小を論じる解き方でも
いいと思います。
ちなみに、冗談の通じない方のために、一応野暮な補足説明をしておきますが、
僕が上でディスった企業は、どれも良い企業です。
東工大 高校数学
さすが東工大。問題がくだらない。
東工大に行く奴なんて、未成年なのにタバコを吸っている不良か、髪の毛がリーゼントの
落ちこぼれか、ニート予備軍ばかりなので、こういう計算するまでもない問題を出さないと、
受験生が答案に何も書けなくなってしまうのでしょう。
2ちゃん(今は「5ちゃんねる」ですが)の有名な信州大コピペにもある通りです。
大体就職先も、
テロリストに爆破されたことがある危険な鉄工所とか、
(僕は個人的には2SC1815とか2SK241とか2SK1530とかは大好きですけど)
不正会計のせいで儲かる事業を売る羽目になった電機会社とか、
聞いたこともない工務店とか、
これまた聞いたこともない電線屋とか、
京都の花札屋みたいな会社とか、
世間一般の価値観で言うなら、ろくなところがありません。
それでも就職できるのはまだいいほうで、僕みたいに対人恐怖だと、くまみこ第11話で、
雨宿まちがセンダイでアイドルコンテストのリハーサルに出たときに、
「す…好きなデザートはなまこプリンですっ!!」
と言ってしまったように、緊張して見当はずれなことを言ってしまうせいか、
面接で弾かれて、どこにも就職できず、ニートまっしぐらです。
そういう人は、仕方がないのでアルバイトをしようとするわけですが、
履歴書に「東工大卒」と書くと、大抵どこでも、嫌な顔をされたり、
「君にはもっといい働き口があるよ~」などと言われて、面接で落とされます。
だからニートのまま。
学歴がスティグマになる大学なんて、東工大くらいのものでしょう。
ビリー・ジョエルの曲に、「Allentown」というのがありますが、
Billy Joel - Allentown (Official Video)
その中で
“So the graduations hang on the wallとあります。「Graduations never helped us at all」なら「役立たず」なので、価値は
But they never really helped us at all”
ゼロです。
ところが、東工大の学歴はスティグマ、つまりマイナスになってしまう
のです。
それと比較すると、例えば、京都大学の工学部は素晴らしい。
アニメ系の作曲家一つ取っても、例えば、神前暁さんのような有名な人がいます。
東工大出身者に、こういう有名な人、いますか? いないでしょ?
それが全ての答えです。
どうでもいい話ですが、電電にいたM、今でも対人恐怖や発達障害などの、弱そうな学生を狙ってパワハラやってるんですか?
あれ、今なら、普通に刑事事件で、警察に通報したら、即逮捕されますよ。
特に、指導教官の変更の書類に署名・捺印を強制するのは、
強要罪に問われます。
東工大内部にしかいたことがない世間知らずだから、わからないんだろうけど。
まあそれはともかく、問題の説明をしましょう。
出題は1977年と古いものです。
m、nは自然数で、m<n、そして、0<x<1。という内容ですが、これは暗算でできます。
(1+x/m^2)^m と (1+x/n^2)^n
の大小を比較する
この式は、
(1+(x/m)/m)^m = (1+(x/m)/m)^(m/(x/m)*(x/m))
= ((1+(x/m)/m)^(m/(x/m)))^(x/m)
と変形できますが、(1+(x/m)/m)^(m/(x/m)) は
自然対数の底eの定義式と似ているので、近似して
e^(x/m)
と変形できます。e^t と t の増加・減少は一致するので、
m が大きくなれば、元の式が小さくなることは自明です。
よって、(1+x/m^2)^m > (1+x/n^2)^n とわかります。
でも、(受験)数学的には、それでは説明不足ということなのかも知れません。
YouTubeの動画の鈴木貫太郎さんのように、いちいち数式をいじって「証明」する
必要があるのでしょう。
もちろん、鈴木貫太郎さんの解き方とは別に、f(y)=(1+x/y^2)^y とおいて、
yについて微分して増減表を書き、f(y) の大小を論じる解き方でも
いいと思います。
ちなみに、冗談の通じない方のために、一応野暮な補足説明をしておきますが、
僕が上でディスった企業は、どれも良い企業です。
PR
計算するまでもない問題・その2
さて、今回の計算の不要な問題は、また鈴木貫太郎さんのYouTubeの動画からです。
信州大 三角関数 高校数学
これが、α=2π/3、β=4π/3なのは、計算するまでもなく自明です。
だから、回答としては、
問題は、これで「数学の採点官が納得してくれるかどうか」ですが…。
こうなってくると、「相手を『不快な』気分にさせない回答をするかどうか」という
問題になり、心理学的な話になってしまいます。
…そうです。人間が社会を構成している以上、真に重要なのは、
「正しいかどうか」ではなく、「相手を不快にさせないこと」だった
のです!!
信州大 三角関数 高校数学
0<α<β<2πという問題ですが、
全ての実数xについて
cos(x) + cos(x+α) + cos(x+β) = 0
が成立するようなα、βの値を求めよ
三相交流に関する知識があれば
これが、α=2π/3、β=4π/3なのは、計算するまでもなく自明です。
だから、回答としては、
「三相交流において、互いの位相が2π/3ずれている3本(+1本)の交流電圧のかかる電線をY-Δ変換すれば、中性点を除去(実際には事故を想定して接地することが多いようですが)でき、電線の本数を4本から3本に減らせる物理的性質から、α=2π/3、β=4π/3は自明である」これで、少なくとも物理学的には誤りではありません。
問題は、これで「数学の採点官が納得してくれるかどうか」ですが…。
こうなってくると、「相手を『不快な』気分にさせない回答をするかどうか」という
問題になり、心理学的な話になってしまいます。
…そうです。人間が社会を構成している以上、真に重要なのは、
「正しいかどうか」ではなく、「相手を不快にさせないこと」だった
のです!!
計算するまでもない問題・その1~数学的証明に潜むあいまいさ、そして出題に隠された政治的意図~
受験(特に大学)の数学では、証明問題が多くなり、単純な計算問題は、
相対的に少なくなってきます。
なので、(受験)数学においては、証明は重要な課題というか、テーマとなってきます。
ところが、この「証明」。一体どこまでやればいいのでしょうか?
12世紀のインドの数学者バスカラは、三平方の定理の証明において、ただ図を描いて
文章は「見よ」とだけしか書かなかったことは有名です。
実際の(受験)数学においても、バスカラと同様に「見よ」とか「自明である」とか書けば、
それで「証明」は終了ってことでいいんでしょうか?
どうもこのあたりには、あいまいさが潜んでいるような気がしてなりません。
これがあいまいだと、個人的には思うわけです。
ところで、数学の問題の中には、基礎的な知識さえあれば、計算するまでもない問題が
存在します。
今回例に挙げるのは、2019年のセンター試験の「数学I」の、第4問の(4)です。
具体的にどういう問題なのかは、↓を参考してください。
https://www.asahicom.jp/edu/center-exam/shiken2019/pdf34MQhg2kGR/suugaku1_04.pdf
内容は統計に関する問題で、「モンシロチョウとツバメの初見日(2017年)の散布図」が
どうのこうの~というものです。
このうち、[カ]、[キ]は、
という、統計に関する基本的な知識があれば、(0)の0、と、計算なしで答えが出ます。
そして[ク]も、計算なしで(1)の1、と答えが出ます。
次の[ケ]の問題は、4つのグラフから、正規化したデータがどれなのかを答える内容となっていますが、
という、これまた統計に関する基本的な知識があれば、正規化したグラフは、
元データと見た目が同じような点の集まりで、なおかつ最大値が標準偏差の1より
大きいことが容易に想像できるので、一瞥して(2)、と答えが出ます。
僕は、この問題の存在を、YouTubeで数学の問題の解説をしている動画を観て
知ったのですが、その解説者は、この問題を【良問!】と絶賛していました。
(その方の名誉のために、リンクは張りません)
と僕は思いましたが、まあ、感想は人それぞれなので、その辺はいいでしょう。
これはセンター試験で、マークシートで回答するので、途中の証明のプロセスは
筆記する必要がありません。
なので、この解き方でも全く問題ないと、僕は思います。
しかし、これが記述式の問題だったら、どうなのか? どこまで「証明」すればいいのか?
という疑問が生じます。
個人的には、上で説明した「統計に関する基本的な知識」をサラッと書いておけば、
それで充分だと思います。
だって、一般的には、数学の証明問題で、「三角関数の加法定理」とか
「合成関数の微分の公式」とか、いちいち証明した上で使ったりしないでしょ?
それは、「数学を勉強してきた人は、そのくらいは知っているだろうから、
自明であるとして断りなしに使っても問題ない」という、暗黙の合意
(数学らしくない、あいまいな合意だと思いますが)があるからでしょう。
だったら、それを統計に適用しても、何ら問題ないはすだ。そういう考えです。
もちろん、初学者に対しては、「なぜそうなるのか?」を論理的に納得させるために、
数式を変形・計算した丁寧な証明を示す必要はあると思います。
以上で「計算するまでもない問題」自体の話は終わりです。ただこの出題については、
もう一つ言いたいことがあります。それは、
という問題です。
昔センター試験(に限らず、入学試験)を受けた経験のある方ならご存知かと思いますが、
昔は、統計分野の問題は、出題されることは、まずありませんでした。
なので、受験生も、統計分野の勉強はしていませんでした。
せいぜい、平均値や分散、標準偏差の定義の式を覚えるくらいでした。
ところが、「ある時期」から、統計に関する問題が、盛んに出題されるようになりました。
具体的に言うと、2010年代以降です。
僕の知っている例だと、大学入試に限らず、神奈川県の公立高校の数学の入試問題にも、
「ある時期」から、統計に関する問題が出題されるようになりました。
この時期については、僕は心当たりがあります。それは、
という本が出版された後、ということです。
特に「子どもが減って何が悪いか!」はインパクトが大きく、内閣府男女共同参画局が、
OECDの統計データ(出生率と女子労働力率)を、自分に都合のいいように捏造した
疑いがあることを、赤川氏自身が統計データを再処理することで示しました。
最近、厚生労働省が各種の統計データを捏造したということで、ニュースになっています。
これに対して、例えば、評論家の三橋貴明氏は、自身のブログで
https://ameblo.jp/takaakimitsuhashi/entry-12435341587.html
と述べていますが、その“重大な国民への裏切り”が“我が国”において“現在”に始まった
話でないことは、この種の問題を扱ったことのある人なら「常識」に属する知識で、
彼ら(お役所)が「結論ありき」でデータを捏造してきた前科があることは、
周知の事実です。
「政治の話は扱わない」と以前書きましたが、それでも僕は、かつて
フェミニズム批判をしたことがありました。
それはなぜかと言うと、三橋氏の述べる通り、その種の捏造が
“重大な国民への裏切り”だからです。
というか、嘘つきに「お前は嘘つきだ」と指摘して批判するのは、
ただの事実の提示であり、「政治の話」以前の問題だと、僕は考えます。
話を戻しましょう。それでは、
なぜセンター試験で統計の問題が出題されるようになったのか?
…おっと! これ以上は政治の話になってしまうので、これ以上のことを書くかどうかは、
後でじっくり考えたいと思います。
最後に、彼ら官僚たちのように、邪な動機で科学を濫用しないための反面教師として。
アラン・ソーカルの「「知」の欺瞞」は良著だと思いますが、内容を理解するのに、
物理学や数学基礎論の知識がある程度必要になり、難しすぎるので、
あまりお勧めしません。
は、高校生くらいでも、知識欲が旺盛な人なら理解できると思うので、おすすめです。
相対的に少なくなってきます。
なので、(受験)数学においては、証明は重要な課題というか、テーマとなってきます。
ところが、この「証明」。一体どこまでやればいいのでしょうか?
12世紀のインドの数学者バスカラは、三平方の定理の証明において、ただ図を描いて
文章は「見よ」とだけしか書かなかったことは有名です。
実際の(受験)数学においても、バスカラと同様に「見よ」とか「自明である」とか書けば、
それで「証明」は終了ってことでいいんでしょうか?
どうもこのあたりには、あいまいさが潜んでいるような気がしてなりません。
「○○を証明せよ」という問題が出題されたら、どこまで証明すればいいのか?
これがあいまいだと、個人的には思うわけです。
ところで、数学の問題の中には、基礎的な知識さえあれば、計算するまでもない問題が
存在します。
今回例に挙げるのは、2019年のセンター試験の「数学I」の、第4問の(4)です。
具体的にどういう問題なのかは、↓を参考してください。
https://www.asahicom.jp/edu/center-exam/shiken2019/pdf34MQhg2kGR/suugaku1_04.pdf
内容は統計に関する問題で、「モンシロチョウとツバメの初見日(2017年)の散布図」が
どうのこうの~というものです。
このうち、[カ]、[キ]は、
統計データを正規化すれば、そのデータの平均は0、分散は(標準偏差も)1
という、統計に関する基本的な知識があれば、(0)の0、と、計算なしで答えが出ます。
そして[ク]も、計算なしで(1)の1、と答えが出ます。
次の[ケ]の問題は、4つのグラフから、正規化したデータがどれなのかを答える内容となっていますが、
- 正規化したデータの最大値(全て同じ値でなければ、それは平均より大きい)と、元データの符号は変わらない
- 分散と平均を持つ統計データを大量に集めると、中心極限定理により、その統計データは正規分布に近づく
- 正規化された正規分布では、標準偏差の範囲内には、(-1<=x<=1)全体の約68.26%のデータが入る
という、これまた統計に関する基本的な知識があれば、正規化したグラフは、
元データと見た目が同じような点の集まりで、なおかつ最大値が標準偏差の1より
大きいことが容易に想像できるので、一瞥して(2)、と答えが出ます。
僕は、この問題の存在を、YouTubeで数学の問題の解説をしている動画を観て
知ったのですが、その解説者は、この問題を【良問!】と絶賛していました。
(その方の名誉のために、リンクは張りません)
…統計の知識があれば、何の計算もなく解ける問題が、良問?
と僕は思いましたが、まあ、感想は人それぞれなので、その辺はいいでしょう。
これはセンター試験で、マークシートで回答するので、途中の証明のプロセスは
筆記する必要がありません。
なので、この解き方でも全く問題ないと、僕は思います。
しかし、これが記述式の問題だったら、どうなのか? どこまで「証明」すればいいのか?
という疑問が生じます。
個人的には、上で説明した「統計に関する基本的な知識」をサラッと書いておけば、
それで充分だと思います。
だって、一般的には、数学の証明問題で、「三角関数の加法定理」とか
「合成関数の微分の公式」とか、いちいち証明した上で使ったりしないでしょ?
それは、「数学を勉強してきた人は、そのくらいは知っているだろうから、
自明であるとして断りなしに使っても問題ない」という、暗黙の合意
(数学らしくない、あいまいな合意だと思いますが)があるからでしょう。
だったら、それを統計に適用しても、何ら問題ないはすだ。そういう考えです。
もちろん、初学者に対しては、「なぜそうなるのか?」を論理的に納得させるために、
数式を変形・計算した丁寧な証明を示す必要はあると思います。
以上で「計算するまでもない問題」自体の話は終わりです。ただこの出題については、
もう一つ言いたいことがあります。それは、
そもそも、なぜセンター試験で統計の問題が出題されるようになったのか?
という問題です。
昔センター試験(に限らず、入学試験)を受けた経験のある方ならご存知かと思いますが、
昔は、統計分野の問題は、出題されることは、まずありませんでした。
なので、受験生も、統計分野の勉強はしていませんでした。
せいぜい、平均値や分散、標準偏差の定義の式を覚えるくらいでした。
ところが、「ある時期」から、統計に関する問題が、盛んに出題されるようになりました。
具体的に言うと、2010年代以降です。
僕の知っている例だと、大学入試に限らず、神奈川県の公立高校の数学の入試問題にも、
「ある時期」から、統計に関する問題が出題されるようになりました。
この時期については、僕は心当たりがあります。それは、
という本が出版された後、ということです。
特に「子どもが減って何が悪いか!」はインパクトが大きく、内閣府男女共同参画局が、
OECDの統計データ(出生率と女子労働力率)を、自分に都合のいいように捏造した
疑いがあることを、赤川氏自身が統計データを再処理することで示しました。
最近、厚生労働省が各種の統計データを捏造したということで、ニュースになっています。
これに対して、例えば、評論家の三橋貴明氏は、自身のブログで
“官僚が不正統計を行い、官僚がチェックし、「組織的隠ぺいはなかった」と一方的に結論付ける。ポスト・トゥルース(中編)
組織的な隠蔽があろうとなかろうと、統計不正は重大な国民への裏切りです。
しかも、厚生労働省が不正調査用の「マニュアル」を作成しておきながら、組織の関与を否定する。
頭がおかしい、としか表現のしようがないのが、現在の我が国です。”
https://ameblo.jp/takaakimitsuhashi/entry-12435341587.html
と述べていますが、その“重大な国民への裏切り”が“我が国”において“現在”に始まった
話でないことは、この種の問題を扱ったことのある人なら「常識」に属する知識で、
彼ら(お役所)が「結論ありき」でデータを捏造してきた前科があることは、
周知の事実です。
「政治の話は扱わない」と以前書きましたが、それでも僕は、かつて
フェミニズム批判をしたことがありました。
それはなぜかと言うと、三橋氏の述べる通り、その種の捏造が
“重大な国民への裏切り”だからです。
というか、嘘つきに「お前は嘘つきだ」と指摘して批判するのは、
ただの事実の提示であり、「政治の話」以前の問題だと、僕は考えます。
話を戻しましょう。それでは、
なぜセンター試験で統計の問題が出題されるようになったのか?
…おっと! これ以上は政治の話になってしまうので、これ以上のことを書くかどうかは、
後でじっくり考えたいと思います。
最後に、彼ら官僚たちのように、邪な動機で科学を濫用しないための反面教師として。
アラン・ソーカルの「「知」の欺瞞」は良著だと思いますが、内容を理解するのに、
物理学や数学基礎論の知識がある程度必要になり、難しすぎるので、
あまりお勧めしません。
は、高校生くらいでも、知識欲が旺盛な人なら理解できると思うので、おすすめです。
1111……111 全ての桁が1の整数には2019の倍数が必ずある→計算してみました
久しぶりの更新です。
さて、今年は2019年となり、御代も新しくなります。(情勢は暗いですが)
YouTubeを観ていたら、鈴木貫太郎さんの、こんな動画を見つけました。
1111……111 全ての桁が1の整数には2019の倍数が必ずある
動画を観れば、その証明がなされているので、理論的には、「1111…111」は、2019(というか、5の倍数以外の奇数)で必ず割り切れることがわかります。
この証明を見ていて思ったのは、「これ、意外と計算量少なくて、実際に求められないかな?」でした。
というわけで、PascalChanの名前に負けないよう(最近は、マイコン開発などでCを使わざるを得ないことが多いのです。残念)、Pascalで計算してみました。
その場合、非常に大きな整数を扱うので、任意精度演算ライブラリ(「BigNum」などと呼ばれているアレ)が必要となります。
ぐぐって調べたところ、Benito van der Zander さんの bigdecimalmath(https://github.com/benibela/bigdecimalmath)が良いようなので、これを使ってみました。
その中にある「bigdecimalmath.pas」を、Lazarusのコンソールアプリのプロジェクトに取り込んで計算しました。ソースはこれです。
その結果、
となりました。「111…11」は、672桁の数でした。
というわけで、今年は、くだらない記事も含めて、いろいろ更新したいと思っています。
さて、今年は2019年となり、御代も新しくなります。(情勢は暗いですが)
YouTubeを観ていたら、鈴木貫太郎さんの、こんな動画を見つけました。
1111……111 全ての桁が1の整数には2019の倍数が必ずある
動画を観れば、その証明がなされているので、理論的には、「1111…111」は、2019(というか、5の倍数以外の奇数)で必ず割り切れることがわかります。
この証明を見ていて思ったのは、「これ、意外と計算量少なくて、実際に求められないかな?」でした。
というわけで、PascalChanの名前に負けないよう(最近は、マイコン開発などでCを使わざるを得ないことが多いのです。残念)、Pascalで計算してみました。
その場合、非常に大きな整数を扱うので、任意精度演算ライブラリ(「BigNum」などと呼ばれているアレ)が必要となります。
ぐぐって調べたところ、Benito van der Zander さんの bigdecimalmath(https://github.com/benibela/bigdecimalmath)が良いようなので、これを使ってみました。
その中にある「bigdecimalmath.pas」を、Lazarusのコンソールアプリのプロジェクトに取り込んで計算しました。ソースはこれです。
その結果、
| 111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111= 2019 * 55032744482967365582521600352209564690991139728138242254141214022343294260084750426503769742997083264542402729624126355181332893071377469594408673160530515656815805404215508227395300203621154586979252655329921303175389356667216994111496340322491882670188762313576578063948049089208078806890099609267514170931704364096637499312090693962907930218479995597380441362610753398271971823234824720708821748940619668702878212536459193219965879698420560233338836607781630069891585493368554289802432447306147157558747454735567662759341808375983710307633041659787573606295745968851466622640471080292774200649386384899014913873754884156072863353695448792031258598866325463650872269 |
となりました。「111…11」は、672桁の数でした。
というわけで、今年は、くだらない記事も含めて、いろいろ更新したいと思っています。
平成26年度・神奈川県の公立高校入試を解いてみた(数学だけ)
さて今年も、朝刊に、平成26年度の神奈川県の公立高校入試問題が入っていたので、
解いてみました。
今年は雪が降っていたため、朝刊が届くの遅い&寝てないという悪条件が重なり、
自己最低記録となりました。(言い訳)
去年と同じく、記述問題が2問あります。
個人的な感想ですが、これは…全体的には、皆さん、時間が足りないのではないか?と
思いました。
去年より、多少詳しく解説します。
問1:計算するだけ。簡単だと思います。
問2:(エ)は、「対称式」と呼ばれているもので、x + y = 2√6、x*y = 2 を先に計算して
おきます。
(ク)は…。これは、解き方がすぐに思いつかなかったら、後回しにすべき問題だと
思います。 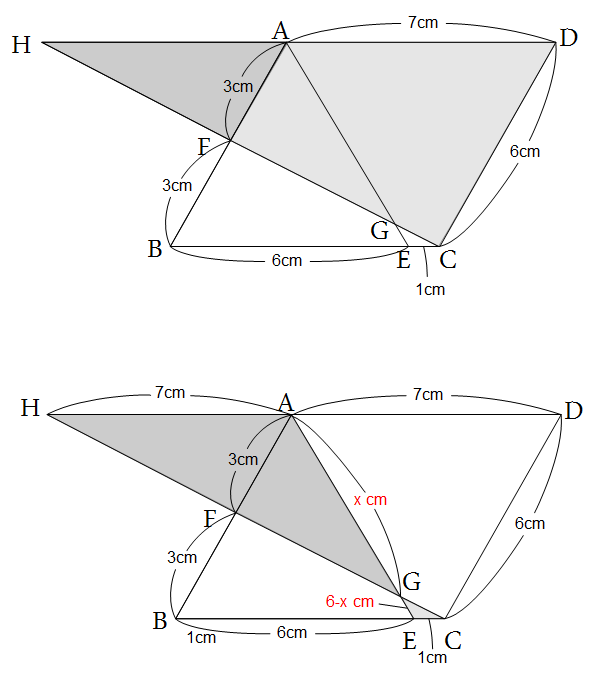 DAを延長し、CFも延長して、できた交点をHとすると、△HAFと△HDAは相似で、
DAを延長し、CFも延長して、できた交点をHとすると、△HAFと△HDAは相似で、
相似比は1:2です。よってHAは7cm。
次に、△HAGと△CEGも相似で、相似比は7:1なので、AG:(6 - AG) = 7:1 となり、
これを解くと、21/4 となります。
問3:(ア)は、点Dの座標を求めれば出せます。まず、y = x^2 の各座標を求めます。
AE:ED = 4:3 より、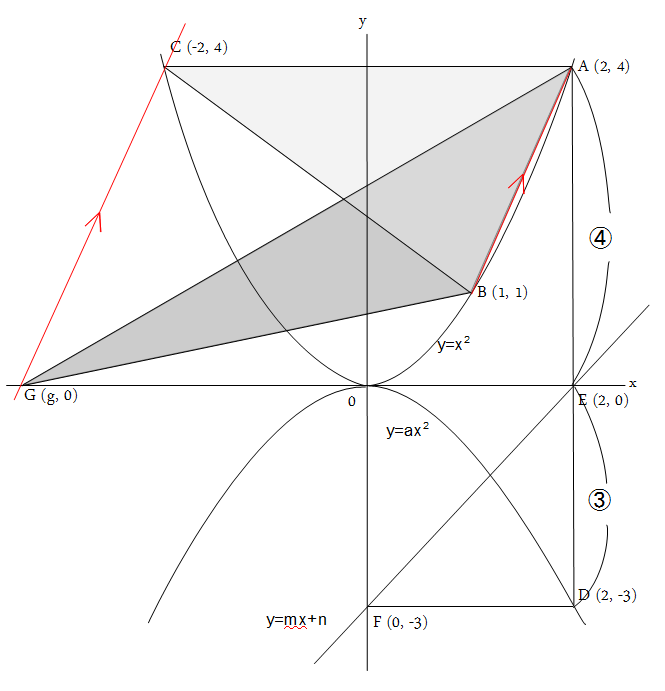 D(2, -3) となるので、これを y = a*x^2 に代入して a を求めると、a = -3/4 と
D(2, -3) となるので、これを y = a*x^2 に代入して a を求めると、a = -3/4 と
出ます。
(イ)は、F(0, -3)、E(2, 0) の2点を通る直線なので、傾きは 3/2、切片は -3 より、
y = 3/2*x - 3 と出せます。
(ウ)は、ここでは「等積変形」を用いるのが定石でしょう。△ABCと△ABGは、
辺ABを共有しているので、辺ABに平行で、点Cを通る直線上に点Gがあれば、
互いの面積は等しくなります。
直線ABの傾きは、計算すると 3 になるので、これと同じ傾きの直線が、
点C(-2, 4)を通ればいいわけです。
y = 3x + b の x, y にこの座標を代入して b を求めると、y = 3x + 10 となります。
後は、y = 0 のときの x が求める点Gのx座標となり、それは -10/3 となります。
よって、G(-10/3, 0)。
問4:この手のさいころを2つ振る問題は、6x6のマトリクスを描いて、そこに値を
書き込むのが定石ですが、この問題に限って言うと、それでは時間がかかって
しまうので、止めるべきでしょう。
(ア)は、2つのさいころの目を足すと、2~12 までの値になるので、該当する
「5の倍数」は、5 と 10 になります。それぞれ、(4, 1), (3, 2), (2, 3), (1, 4) と
(6, 4), (5, 5), (4, 6) があるので、合計7通り。よって答えは 7/36。
(イ)は、210 を素因数分解すると、2*3*5*7 と、何だか素数を並べたような作為的な
数字が出てきます。これを組み合わせて 11~66 までの数を作ると、
(2, 3, 5), (2, 3, 7), (2, 7), (3, 5), (3, 7), (5, 7) の組み合わせが考えられます。
しかし!
(2, 3, 5) は、30 となるので、1の位が0になってしまい、さいころ的に
ありえません。なので、これを除くと、答えは 5/36。
(ウ)は、111 = 3*37 と、これまた作為的な数字が出てきます。よって
ルートの中は、3*(37 - n) となります。これの (37 - n) が、
3*1^2 = 3 、3*2^2 = 12 、3*3^2 = 27 、3*4^2 = 48 … となればいいわけ
ですが、さいころの目からして、36より大きい数の 48 以降はありえないので、
合計3つということになり、答えは 3/36 = 1/12。
(n は計算しないように。時間の無駄です)
問5:これは、書くのに時間がかかります。それと、問題の文章から式を立てるのが苦手な
人には、解けない問題だと思います。しかし内容は、単なる連立方程式です。
Aさんが、家からC商店まで上昇するのに x/50 分、C商店からBさんの家まで
下降するのに y/60 分、勉強したのが 60 分、Bさんの家からC商店まで上昇したのが
y/50 分、C商店で 5 分、そして、再びC商店からBさんの家まで下降するのに
y/60 分かかっています。
8時から9時39分までは、1時間39分 = 99 分。
つまり、
x/50 + y/60 + 60 + y/50 + 5 + y/60 = 99 …(1)
変形すると、
x/50 + y/30 + y/50 = 34, 3*x + 5*y + 3*y = 34*150,
3*x + 8*y = 5100 …(2)
一方、距離で言うと、x + y = 1200 …(3)
なので、(2) と (3) を連立方程式で解くと、x = 900, y = 300 メートルと出ます。
問6:(ア)は、計算するだけです。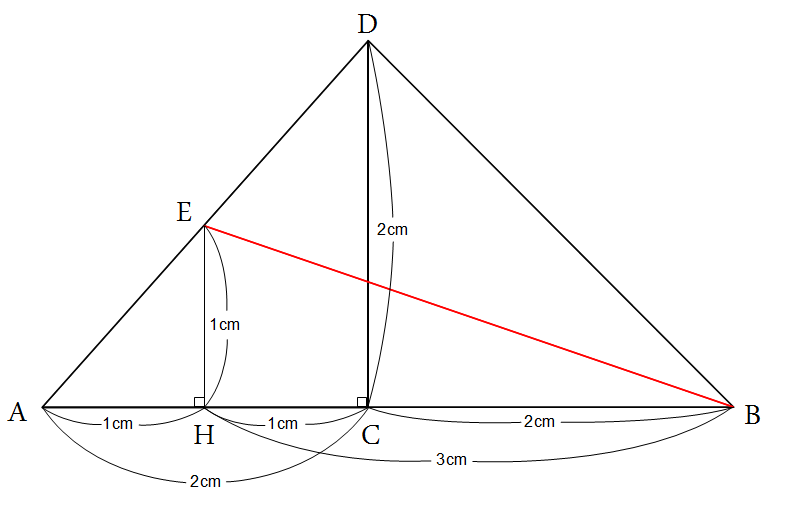 (イ)は、上の展開図のように考えると、EH^2 = 1、BH^2 = 9 となるので、
(イ)は、上の展開図のように考えると、EH^2 = 1、BH^2 = 9 となるので、
BE = √10。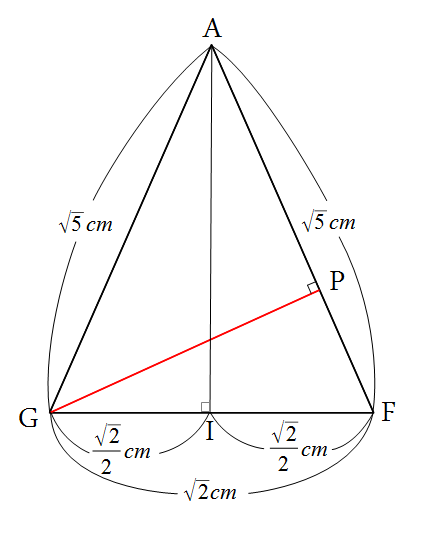 (ウ)は、△AGFが、上の図のような二等辺三角形になることを考えると、
(ウ)は、△AGFが、上の図のような二等辺三角形になることを考えると、
AI^2 = 5 - 1/2 = 9/2、
AI = 3/√2 となるので、△AGFの面積は、√2*3/√2/2 = 3/2 となります。
ここで、AFを底辺と見ると、√5xGP/2 = △AGF = 3/2 なので、
GP = 3/√5 = 3√5/5。
問7:公表された答えとは異なっていましたが、合っているはずです。
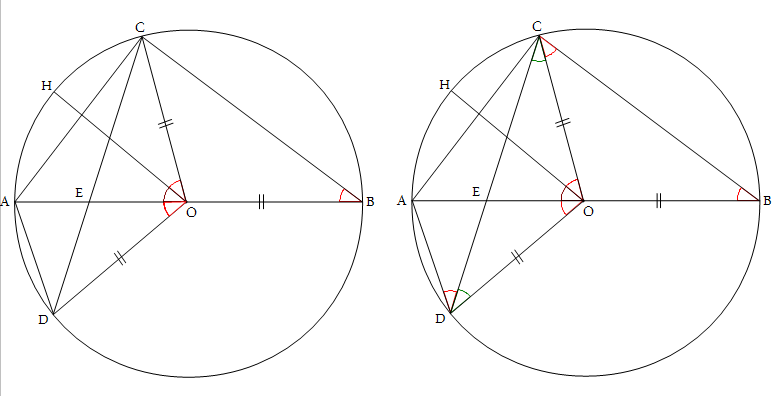
まず、∠COAの二等分線を引き、それと弧ACが交わる点を、H とします。
円周角の性質と仮定から、∠DOA = ∠HOA = ∠COH = ∠CBA …(1)
弧CAに対する円周角なので、∠CBA = ∠CDA …(2)
△OBCは二等辺三角形なので、∠CBA = ∠OCB …(3)
△OCDも二等辺三角形なので、∠OCD = ∠ODC …(4)
∠ODA = ∠ODC + ∠ODC …(5)
∠BCA = ∠OCB + ∠OCD …(6)
(3)、(4) から (5)、(6) は、∠ODA = ∠BCA …(7)
(1)、(2)、(7) より、対応する2つの角が等しいので、△OAD ∽ △BCE。
※弧DBに対する円周角から、∠OAD = ∠BCE とやったほうが速い。これが、
公表された答えです。
ちなみに僕は、解くのに50分では足りませんでした。結果は74点。
今まで解いた中で、最低の得点率でした。
問5の立式にケアレスミスがあり、それだけで10点全て落としてしまいました。
その他、確率の問題を読み間違えていたりと、散々でした。
睡眠はよく取りましょう。
解いてみました。
今年は雪が降っていたため、朝刊が届くの遅い&寝てないという悪条件が重なり、
自己最低記録となりました。(言い訳)
去年と同じく、記述問題が2問あります。
個人的な感想ですが、これは…全体的には、皆さん、時間が足りないのではないか?と
思いました。
去年より、多少詳しく解説します。
問1:計算するだけ。簡単だと思います。
問2:(エ)は、「対称式」と呼ばれているもので、x + y = 2√6、x*y = 2 を先に計算して
おきます。
そして、x^2*y + x*y^2 = xy(x + y) と因数分解して代入すれば、4√6 と出ます。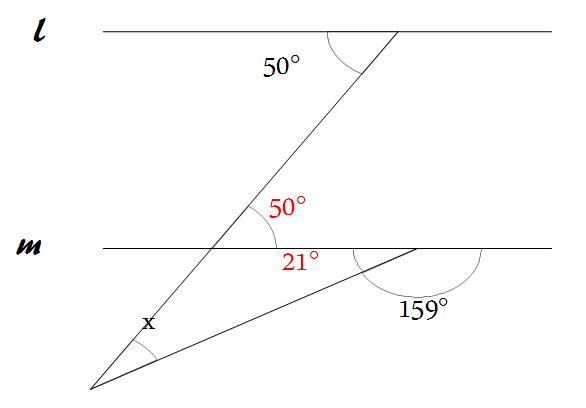
(キ)は、上の図のように角度を求めれば、x = 50°- 21°= 29°と出ます。(ク)は…。これは、解き方がすぐに思いつかなかったら、後回しにすべき問題だと
思います。
相似比は1:2です。よってHAは7cm。
次に、△HAGと△CEGも相似で、相似比は7:1なので、AG:(6 - AG) = 7:1 となり、
これを解くと、21/4 となります。
問3:(ア)は、点Dの座標を求めれば出せます。まず、y = x^2 の各座標を求めます。
AE:ED = 4:3 より、
出ます。
(イ)は、F(0, -3)、E(2, 0) の2点を通る直線なので、傾きは 3/2、切片は -3 より、
y = 3/2*x - 3 と出せます。
(ウ)は、ここでは「等積変形」を用いるのが定石でしょう。△ABCと△ABGは、
辺ABを共有しているので、辺ABに平行で、点Cを通る直線上に点Gがあれば、
互いの面積は等しくなります。
直線ABの傾きは、計算すると 3 になるので、これと同じ傾きの直線が、
点C(-2, 4)を通ればいいわけです。
y = 3x + b の x, y にこの座標を代入して b を求めると、y = 3x + 10 となります。
後は、y = 0 のときの x が求める点Gのx座標となり、それは -10/3 となります。
よって、G(-10/3, 0)。
問4:この手のさいころを2つ振る問題は、6x6のマトリクスを描いて、そこに値を
書き込むのが定石ですが、この問題に限って言うと、それでは時間がかかって
しまうので、止めるべきでしょう。
(ア)は、2つのさいころの目を足すと、2~12 までの値になるので、該当する
「5の倍数」は、5 と 10 になります。それぞれ、(4, 1), (3, 2), (2, 3), (1, 4) と
(6, 4), (5, 5), (4, 6) があるので、合計7通り。よって答えは 7/36。
(イ)は、210 を素因数分解すると、2*3*5*7 と、何だか素数を並べたような作為的な
数字が出てきます。これを組み合わせて 11~66 までの数を作ると、
(2, 3, 5), (2, 3, 7), (2, 7), (3, 5), (3, 7), (5, 7) の組み合わせが考えられます。
しかし!
(2, 3, 5) は、30 となるので、1の位が0になってしまい、さいころ的に
ありえません。なので、これを除くと、答えは 5/36。
(ウ)は、111 = 3*37 と、これまた作為的な数字が出てきます。よって
ルートの中は、3*(37 - n) となります。これの (37 - n) が、
3*1^2 = 3 、3*2^2 = 12 、3*3^2 = 27 、3*4^2 = 48 … となればいいわけ
ですが、さいころの目からして、36より大きい数の 48 以降はありえないので、
合計3つということになり、答えは 3/36 = 1/12。
(n は計算しないように。時間の無駄です)
問5:これは、書くのに時間がかかります。それと、問題の文章から式を立てるのが苦手な
人には、解けない問題だと思います。しかし内容は、単なる連立方程式です。
Aさんが、家からC商店まで上昇するのに x/50 分、C商店からBさんの家まで
下降するのに y/60 分、勉強したのが 60 分、Bさんの家からC商店まで上昇したのが
y/50 分、C商店で 5 分、そして、再びC商店からBさんの家まで下降するのに
y/60 分かかっています。
8時から9時39分までは、1時間39分 = 99 分。
つまり、
x/50 + y/60 + 60 + y/50 + 5 + y/60 = 99 …(1)
変形すると、
x/50 + y/30 + y/50 = 34, 3*x + 5*y + 3*y = 34*150,
3*x + 8*y = 5100 …(2)
一方、距離で言うと、x + y = 1200 …(3)
なので、(2) と (3) を連立方程式で解くと、x = 900, y = 300 メートルと出ます。
問6:(ア)は、計算するだけです。
BE = √10。
AI^2 = 5 - 1/2 = 9/2、
AI = 3/√2 となるので、△AGFの面積は、√2*3/√2/2 = 3/2 となります。
ここで、AFを底辺と見ると、√5xGP/2 = △AGF = 3/2 なので、
GP = 3/√5 = 3√5/5。
問7:公表された答えとは異なっていましたが、合っているはずです。
まず、∠COAの二等分線を引き、それと弧ACが交わる点を、H とします。
円周角の性質と仮定から、∠DOA = ∠HOA = ∠COH = ∠CBA …(1)
弧CAに対する円周角なので、∠CBA = ∠CDA …(2)
△OBCは二等辺三角形なので、∠CBA = ∠OCB …(3)
△OCDも二等辺三角形なので、∠OCD = ∠ODC …(4)
∠ODA = ∠ODC + ∠ODC …(5)
∠BCA = ∠OCB + ∠OCD …(6)
(3)、(4) から (5)、(6) は、∠ODA = ∠BCA …(7)
(1)、(2)、(7) より、対応する2つの角が等しいので、△OAD ∽ △BCE。
※弧DBに対する円周角から、∠OAD = ∠BCE とやったほうが速い。これが、
公表された答えです。
ちなみに僕は、解くのに50分では足りませんでした。結果は74点。
今まで解いた中で、最低の得点率でした。
問5の立式にケアレスミスがあり、それだけで10点全て落としてしまいました。
その他、確率の問題を読み間違えていたりと、散々でした。
睡眠はよく取りましょう。
- 1
- 2
忍者カウンター
カレンダー
最新記事
(05/08)
(04/10)
(03/26)
(03/22)
(03/12)
プロフィール
HN:
PascalChan
性別:
男性
趣味:
引きこもり
ブログ内検索
P R
